曾工致力于各类电子电器产品的国际国内认证、EMC整改,欢迎各位询价,提供专业服务,解决客户痛点!专治各种产品不合格!
电话:139 2899 3907 邮箱:info@emc.wiki
“三角函数”的版本间差异
| 第34行: | 第34行: | ||
===直角坐标系中的定义=== | ===直角坐标系中的定义=== | ||
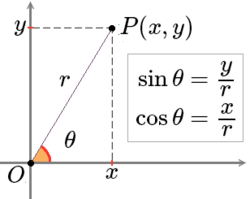
设P(x,y)是平面直角坐标系xOy中的一个点,详细如右图(或上图)所示。 | 设P(x,y)是平面直角坐标系xOy中的一个点,详细如右图(或上图)所示。 | ||
| 第52行: | 第51行: | ||
|cscθ =r/y | |cscθ =r/y | ||
|} | |} | ||
[[文件:Trig functions on descartes.png|thumb|250px]] | |||
这样可以对0到360度的角度定义三角函数。要注意的是以上的定义都只在定义式有意义的时候成立。比如说当x=0 的时候,y/x和r/x都没有意义,这说明对于90度角和270度角,正切和正割没有定义。同样地,对于0度角和180度角,余切和余割没有定义。 | 这样可以对0到360度的角度定义三角函数。要注意的是以上的定义都只在定义式有意义的时候成立。比如说当x=0 的时候,y/x和r/x都没有意义,这说明对于90度角和270度角,正切和正割没有定义。同样地,对于0度角和180度角,余切和余割没有定义。 | ||
===单位圆定义=== | |||
[[文件:Trig functions on unit circle.png|thumb|right|240px|用单位圆定义三角函数]] | |||
三角函数也可以依据直角坐标系xOy中半径为1,圆心为原点O的单位圆来定义。 | |||
2020年8月2日 (日) 15:58的版本
三角函数
三角函数(英语:Trigonometric functions)是数学中常见的一类关于角度的函数。三角函数将直角三角形的内角和它的两个边的比值相关联,也可以等价地用与单位圆有关的各种线段的长度来定义。三角函数在研究三角形和圆等几何形状的性质时有重要作用,也是研究振动、波、天体运动以及各种周期性现象的基础数学工具。在数学分析中,三角函数也被定义为无穷级数或特定微分方程的解,允许它们的取值扩展到任意实数值,甚至是复数值。
常见的三角函数包括正弦函数(sin)、余弦函数(cos)和正切函数(tan或者tg);在航海学、测绘学、工程学等其他学科中,还会用到如余切函数(cot或者ctg)、正割函数(sec)、余割函数(csc )、正矢函数、半正矢函数等其他的三角函数。不同的三角函数之间的关系可以通过几何直观或者计算得出,称为三角恒等式。
三角函数一般用于计算三角形中未知长度的边和未知的角度,在导航、工程学以及物理学方面都有广泛的用途。另外,以三角函数为模版,可以定义一类相似的函数,叫做双曲函数。常见的双曲函数也被称为双曲正弦函数、双曲余弦函数等等。
几何定义
直角三角形中的定义
在直角三角形中仅有锐角(大小在0到90度之间的角)三角函数的定义。给定一个锐角θ,可以做出一个直角三角形,使得其中的一个内角是θ。设这个三角形中,θ的对边、邻边和斜边长度分别是a, b, h,那么
- θ的正弦是对边与斜边的比值:sinθ=a/h
- θ的余弦是邻边与斜边的比值:cosθ=b/h
- θ的正切是对边与邻边的比值:tanθ=a/b
- θ的余切是邻边与对边的比值:cotθ=b/a
- θ的正割是斜边与邻边的比值:secθ=h/b
- θ的余割是斜边与对边的比值:cscθ=h/a
直角坐标系中的定义
设P(x,y)是平面直角坐标系xOy中的一个点,详细如右图(或上图)所示。
| 正弦 | 余弦 | 正切 | 余切 | 正割 | 余割 |
|---|---|---|---|---|---|
| sinθ =y/r | cosθ =x/r | tanθ =y/x | cotθ =x/y | secθ =r/x | cscθ =r/y |
这样可以对0到360度的角度定义三角函数。要注意的是以上的定义都只在定义式有意义的时候成立。比如说当x=0 的时候,y/x和r/x都没有意义,这说明对于90度角和270度角,正切和正割没有定义。同样地,对于0度角和180度角,余切和余割没有定义。
单位圆定义
三角函数也可以依据直角坐标系xOy中半径为1,圆心为原点O的单位圆来定义。